Twin Paradox Explained. Simples.

The Twin Paradox - Probably the most well known of all the supposed paradoxes associated with Special Relativity.

So what is it?

In 1911, Paul Langevin first proposed it as an attempt to visualize effects of a journey at near Light Speed, utilising the additional twist of making the subjects twins, thereby emphasizing the paradoxical nature of the effect.  It was the tale of a traveller taking a trip at the Lorentz Factor, ɣ = 100. (v = 99.98c) He travels for one year of his time, stops and then reverses direction. On his return, the traveller will have aged two years, while 200 years have passed on Earth.

This was very much in accord with the visualization of Special Relativity, enjoyed by Einstein himself. 

In order to see this effect more easily we will choose a much lower value for ɣ of 1.25 (v = 0.6c)as that will show the relationship more clearly using our new diagram:

Outgoing Journey

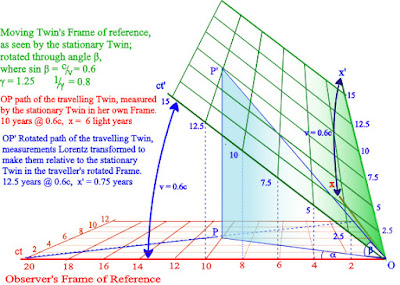
Fig. 1 21 Twins Rotated Frames (1)

In Fig 13 we see the path of the travelling twin as seen by his sibling, travelling 6 light years (x axis) in ten years (v = 0.6c) as measured by the Resting Twin in her Frame of Reference; but in the Traveller's green, rotated Frame, we see that she will measure that he has travelled 7.5 light years in 12.5 years (again v= 0.6c).  

Dilated Time	Contracted Length
t' = γt	x = x'/γ
t' = 1.25 * 10	x = 7.5/1.25
t' = 12.5 years	x = 6 light years

Both changes functions of the Lorentz factor of 1.25. 

Turnaround Point

Fig. 2 Twins Rotated Frames (2)

This brings us to the next significant point in the Traveller's journey, the turnaround point, where he slows down to rest relative to the Resting Twin, and therefore joins her in the one Frame of Reference.  v = 0, Lorentz factor = 1.  All measurements will be the same wherever they are measured from.

t' = t

x = x'

No Time dilation, no length contraction.

And note that the angle of rotation β which represents the velocity will also have reduced to zero.

Return Trip

Fig. 3 Twins Rotated Frames (3)

On the return trip we see the moving Frame rotated in the opposite direction as the relative velocity v = -0.6c. 

It is important to recognize that, as a form of Minkowski diagram, in which the current velocity is shown by rotation about the point of departure O; acceleration changes the angle of rotation for that current velocity, i.e. for the whole journey.  There are not, nor ever can be, changes within the length of that line, it is always a simple straight line, no kinks or bends.

So we see, 

1. OP_O', outgoing, v = 0.6c, decelerating to;

2. P, turnaround, v = 0,  then acceleration to; 

3. P_R'D', returning, v = -0.6c, followed by the return to rest; 

4. D, home again, v = 0, 

giving us the journey as OPD in the stationary Twin's Frame and OP_O'PP_R'D'D in the traveller's Frame Transformed to be relative to the stationary Twin.  Returning to D the twins are at rest with one another, in a single Frame, once more.  

Which leads to the inevitable conclusion that there is a fault in Paul Langevin's, and, apparently Einstein's, visualization of the Twin Paradox.  It is quite evident now that there is nothing whatsoever Paradoxical in this thought experiment when taken to it's logical conclusion.  

The apparent difference in ageing can only be evident if the traveller were to continue past his sibling and not return to rest; for the Age Difference, an effect of Time Dilation, only exists while there is a relative velocity; Time Dilation (and of course, Length Contraction) being effects of the relative velocity, only exist while their is a relative velocity.

They are effects of that relative velocity, of the relative velocity that exists at that moment; not of how long that relative velocity existed, nor of what other relative velocities prevailed before that moment.

Again, I reiterate: when v = 0, the Lorentz Factor is 1 and time dilation cannot occur.